Octal(8진수)과 Decimal(10진수) 간의 변환 방법은 다음과 같습니다:
하나의 숫자 체계를 다른 체계로 변환하는 대화에 들어가기 전에, 우선 숫자 체계에 대해 약간 이야기해 보겠습니다. 숫자 체계는 서로 다른 조합의 기호들로 정의될 수 있으며, 각 기호마다 특정한 가중치를 가지고 있습니다. 모든 숫자 체계는 기수 또는 체계가 구성된 기준인 진수에 따라 구별됩니다. 기수 또는 진수는 특정 숫자 체계에서 사용되는 서로 다른 기호의 총 개수를 정의합니다. 예를 들어, 이진 숫자 체계의 진수는 2, 십진 숫자 체계의 진수는 10, 팔진 숫자 체계의 진수는 8입니다.
8진수 체계:
이름에서 명확히 알 수 있듯이, 이 숫자 체계는 기수가 8인 것을 기반으로 합니다. 따라서, 이 숫자 체계에서는 여덟 개의 구별되는 숫자가 있습니다. 용이성을 위해, 우리는 이 여덟 개의 숫자를 십진수 체계에서 처음 여덟 개의 숫자와 동일하다고 간주합니다. 각 팔진수 자릿수의 위치는 왼쪽 위치에서 숫자의 색인에 해당하는 8의 거듭제곱과 연결됩니다. 이진 형태로 나타내면 하나의 팔진수를 나타내는 데 최대 세 개의 이진 숫자가 필요합니다. 이 숫자 체계 자체의 기저는 2의 거듭제곱이므로, 컴퓨터에서 사용되는 이진 또는 16진수 숫자 체계로 팔진수를 쉽고 편리하게 상호변환할 수 있습니다.
8진수는 컴퓨터 기계에서 직접적인 응용이 없습니다. 컴퓨터는 이진 상태 또는 비트로 작동하기 때문입니다. 그러나 8진수는 2진으로 표현될 때 더 적은 자릿수를 차지하므로 BCD(이진 부호화 10진수)와 같이 메모리에 공간을 낭비하지 않고 효율적으로 컴퓨터에 저장될 수 있습니다.
10진수를 8진수로 변환하는 방법:
소수를 8진수로 변환하는 방법은 이진수로 변환하는 것과 매우 유사합니다. 유일한 차이점은 이번에는 2대신 8로 소수를 나누는 것입니다. 아래에 작성된 단계를 따라 소수를 변환할 수 있습니다:
- 단계 1: 소수를 8로 나눈 뒤 나머지를 기록하고 값 R1에 할당하십시오. 마찬가지로 몫을 기록하고 값 Q1에 할당하십시오.
- 단계2: Q1을 8로 나누고, 나머지와 몫을 기록하세요. 이 단계에서 얻은 나머지와 몫을 R2와 Q2에 할당하세요.
- 단계 3: 몫(Qn)의 값이 0이 될 때까지 시퀀스를 반복합니다.
- 단계 4: 8진수 숫자는 다음과 비슷합니다: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
예시: 십진수 2181을 고려해 봅시다.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
So, the OCTAL equivalent of 2181 is: 2181의 8진수 변환 결과는:
(2181) Decimal = (4205) Octal
8진수를 2진수로 변환하는 방법:
다시 말하지만, 8진법을 10진법으로 변환하는 것은 2진법을 10진법으로 변환하는 것과 매우 유사합니다. 유일한 차이점은 이번에는 숫자를 2가 아닌 8의 거듭제곱과 곱한다는 것입니다. 변환은 아래에 쓰인 단계를 따라 수행할 수 있습니다: 단계 1: 단계 2: 단계 3: 단계 4: 단계 5: 단계 6: 단계 7: 단계 8: 단계 9: 단계 10: 단계 11: 단계 12: 단계 13: 단계 14: 단계 15: 단계 16: 단계 17: 단계 18: 단계 19: 단계 20: 단계 21: 단계 22: 단계 23: 단계 24: 단계 25: 단계 26: 단계 27: 단계 28: 단계 29: 단계 30: 단계 31: 단계 32: 단계 33: 단계 34: 단계 35: 단계 36: 단계 37: 단계 38: 단계 39: 단계 40: 단계 41: 단계 42: 단계 43: 단계 44: 단계 45: 단계 46: 단계 47: 단계 48: 단계 49: 단계 50:
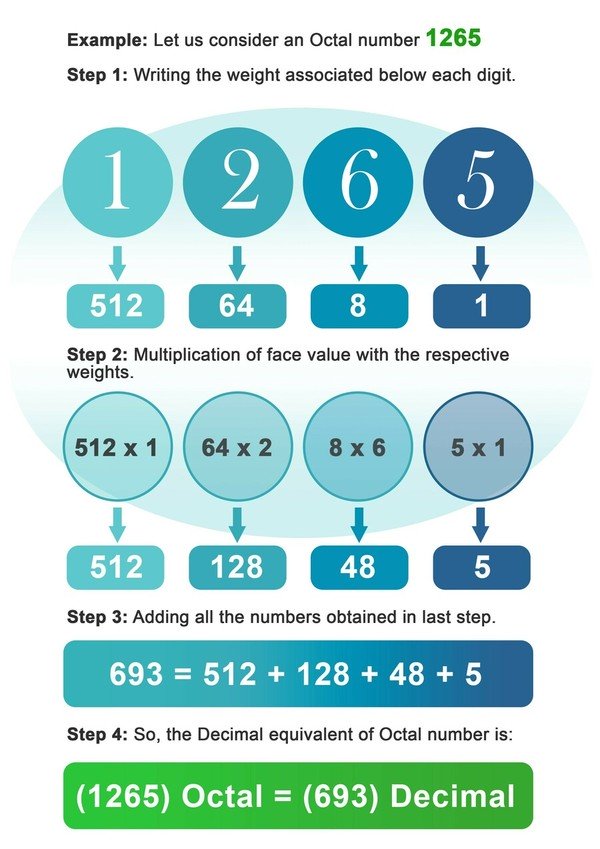
- 단계 1: 8진수 숫자 각 숫자 아래에 연결된 8의 가중치를 적으세요.
- 단계 2: 이제 각 자릿수를 해당 위치 또는 자릿수의 가중치와 곱하세요.
- 단계 3: 이전 단계에서의 곱셈으로 얻은 모든 숫자를 더하세요.
- 단계 4: 마지막 단계에서 얻은 숫자가 8진수의 소수로 대응됩니다.
예시: 8진수 숫자 1265를 고려해 봅시다.