How to convert between the Octal and Decimal Number Systems?
Before getting into the conversation of conversion of one number system into other, let us talk a bit about the Number System itself. Number System can be defined as the set of the different combinations of symbols, with each symbol having a specific weight. Any Number System is differentiated on the basis of the radix or the base on which the number system is made. Radix or the Base defines the total no of different symbols, which is used in a particular number system. For example, the radix of Binary number system is 2, the radix of decimal number system is 10, and the radix of octal number system is 8.
The Octal Number System:
As the name clearly signifies, this number system is based on radix equal to 8. So, in this number system we have eight distinct digits. For ease we consider these eight digits as same as first eight digits in decimal number system. Position of each octal digit is associated with some power of 8 and this power equal the index of the digit from the left position. It takes at max three binary digits to represent one octal number in binary form. As the base of this number system itself is some power of two so, it is very easy and convenient to interconvert octal number into binary or hexadecimal number system which are used in computers to do all of the work.
Octal numbers do not find direct application in the computer machinery because computers work on binary states or bits. However, as the octal number occupy less digit to be represented in binary so they can be efficiently stored in the computer without any wasted space in memory like BCD(Binary Coded Decimal) number.
Conversion of Decimal to Octal Number System:
The conversion of decimal to octal is very similar to converting decimal into binary. The only difference is, this time we will divide the decimal number with 8 instead of 2. The conversion can be done by following the below written steps:
- Step1: Divide the decimal number by 8, note the remainder and assign the value R1 to it. Similarly, note the quotient and assign the value Q1 to it.
- Step2: Now divide Q1 with 8, note the remainder and quotient. Assign the value R2 and Q2 to the remainder and quotient obtained in this step.
- Step3: Repeat the sequence till you get the value of quotient (Qn) equal to 0.
- Step4: The octal number will look something like this : Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Example: Let us consider a decimal number 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
So, the OCTAL equivalent of 2181 is:
(2181) Decimal = (4205) Octal
Conversion of Octal into Binary Number System:
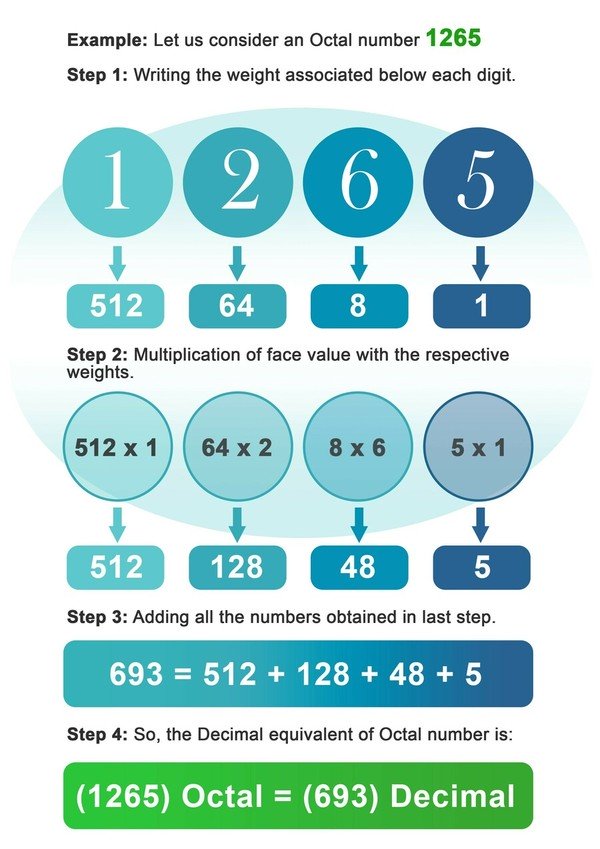
Again, conversion of octal into decimal is very similar to the conversion of binary into decimal, the only difference is that this time we will multiply the digits with the powers of 8 instead of 2. The conversion can be done by following the below written steps:
- Step 1: Write down the weight of 8 associated below every digit of octal number.
- Step2: Now multiply each digit with the weight associated at that place or index of digit.
- Step3: Add all the numbers obtained after multiplication in the previous step.
- Step4: The number obtained in the last step is the decimal equivalent of the octal number.
Example: Let us consider an Octal number 1265.